Что придумал Пифагор

Все знают, что он был ученым и, в частности, автором знаменитой теоремы. А то, что он был еще и блестящим музыкантом, известно не так широко. Сочетание этих дарований позволило Пифагору первым догадаться о существовании природного звукоряда. Но надо было еще доказать это. Пифагор построил для своих экспериментов полуинструмент, полуприбор - монохорд. Это был продолговатый ящик с натянутой поверх него струной. Под струной, на верхней крышке ящика, Пифагор расчертил шкалу, чтобы удобнее было зрительно делить струну на части. Множество опытов проделал Пифагор с монохордом и в конце концов описал математически поведение звучащей струны. Опыты Пифагора легли в основу науки, которую мы называем сейчас музыкальной акустикой.

Пифагору принадлежит и математическое объяснение основ гармонии. Следуя собственной теории совершенства малых чисел, он определял суть гармонии так: наиболее естественно воспринимаются ухом частоты, которые находятся между собой в простых числовых соотношениях. Вот откуда и октава 1:2, и трезвучие 4:5:6.

Когда древнегреческие музыканты ввели пять дополнительных звуков и убедились, что проблема все же осталась, Пифагор взялся за решение уже не теоретической, а сугубо практической задачи: как настроить инструмент, чтобы не увеличивать количество звуков в каждой октаве сверх двенадцати и в то же время дать возможность музыкантам свободнее переходить из тональности в тональность и из лада в лад?

Внутри октавы наиболее слитно с начальным звуком воспринимается квинта, которая составляет с ним тоже простейшее после октавы соотношение - 3:2. Пифагор решил поэтому взять квинту за основу строя и вывел удивительно красивую формулу - полюбуйтесь ею. Но поскольку внешняя красота пока мало о чем говорит, восстановим расчеты Пифагора. Пусть вас не смущают показатели степени в формуле - все опять же сводится к арифметике.

Обратимся к очередной таблице.

Формула музыкального строя, выведенная Пифагором

Подставляем вместо единицы частоту 384 - правую границу уже хорошо знакомой нам октавы. Условно обозначаем ее до. Вправо от до квинта, то есть пятый звук, считая только основные, а вместе с дополнительными восьмой, будет соль. Частота его - три вторых от 384, то есть 576. Квинта от соль - ре. Частота три вторых от 576-864. И так далее, вплоть до фа-диез.

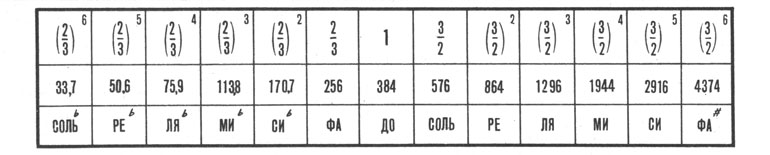
Расшифровка формулы Пифагора

Влево от до квинта - фа. Частота две трети от 384-255,9. Квинта от фа - си-бемоль. Частота две трети от 255,9-170,6. И так до соль-бемоль.

Мы получили ряд из тринадцати частот. Тринадцати, а не двенадцати, потому что крайние справа и слева частоты принадлежат одному и тому же звуку: фа-диез - то же самое, что соль-бемоль.

Теперь этот ряд частот, который охватывает почти весь музыкальный диапазон, нам предстоит свести в одну октаву, то есть последовательным умножением или делением на два (отчего, как мы знаем, название звука не меняется) уложить в промежуток между 192 и 384. Если какая-то частота после умножения или деления на два не улеглась в границы октавы, нужно еще раз умножить или разделить ее на два.

После этих действий мы получим октаву, к которой пришел Пифагор.

Рассматривая ее основные частоты, вы увидите небольшие расхождения с прежним, идеально чистым строем. Вместо частоты 240 появилась частота 243, вместо 320-324, а 360 превратилось в 364,5.

Эти незначительные изменения произвели революцию в музыкальном строе. Интервалы более или менее выровнялись. Определились точные частоты дополнительных звуков. Музыканты, пользуясь теми же двенадцатью звуками в октаве, получили возможность переходить из тональности в тональность гораздо свободнее. Поэтому Пифагоров строй продержался больше двух тысяч лет.

Прежний конфликт музыканта с инструментом был улажен.

Однако наметился новый.

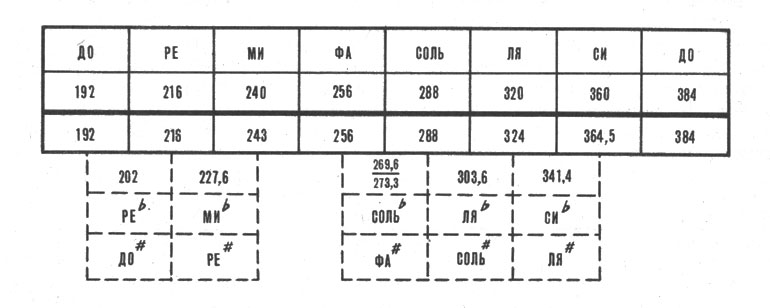
Вверху - уже знакомая нам «чистая» октава. Внизу - октава, к которой пришел Пифагор. Видно, что немного изменились три частоты. Зато настраивать инструменты стало значительно проще. В пунктирных клеточках даны частоты дополнительных звуков. Попутное открытие Пифагора: пониженный звук не равен повышенному предыдущему

Обратите внимание на то, что в Пифагоровом строе между фа и соль стоят две частоты. Когда мы последовательным делением на два привели крайнюю правую частоту фа-диез в нашу октаву, получилось одно число. А когда последовательным умножением на два привели в нашу октаву крайнюю левую частоту си-бемоль, получилось другое. Это было попутное открытие Пифагора: пониженный звук не равен повышенному предыдущему. В нашем примере соль-бемоль не равно фа-диез. Если вы продлите по квинтам формулу Пифагора вправо еще на четыре элемента - до-диез, соль-диез, ре-диез и ля-диез - и самостоятельно проделаете все знакомые уже арифметические операции, то убедитесь, что это открытие справедливо для любого дополнительного звука.

Но чтобы не добавлять новые струны, это противоречие разрешили просто: усреднили две частоты и оставили, как и было, между двумя основными звуками один дополнительный. Усреднение это стало традиционным, так что и сейчас, например, пианист вынужден пользоваться одной черной клавишей там, где, согласно точным акустическим расчетам, их должно быть две. А вот скрипач может по-разному взять соль-бемоль и фа-диез, как и другие повышенные и пониженные звуки. Может взять их по-разному и тромбонист - кулиса его инструмента передвигается совершенно свободно.

Усреднение двух близких частот совершенно незаметно для слушателя с обычным слухом, и не в этом суть нового конфликта. Он выявится, если мы подойдем к расчетам Пифагора с другой стороны.

Когда мы располагали звуки по квинтам, самая левая частота соль-бемоль получилась у нас 33,7, а самая правая частота фа-диез - 4374. Давайте попробуем пройти от первого ко второму октавами, то есть последовательным умножением на два. После семи умножений получим число 4313,6. Как видим, оно существенно расходится с 4374 - на шестьдесят герц. А ведь мы имеем дело с одним и тем же звуком. Выходит, целое число квинт не укладывается в целое число октав. Это расхождение называется Пифагоровой коммой. Комма и привела к конфликту.

О лютнистах эпохи Возрождения шутливо говорили так: если они живут шестьдесят лет, то двадцать из них настраивают свой инструмент. Эта шутка основана на действительном явлении. На грифе лютни первое время не было врезанных намертво порожков, гриф просто перевязывался в определенных местах тонким шнурком или жилами. Эти перевязки и образовывали порожки, которые могли передвигаться по грифу. И вот музыканты, так и этак передвигая порожки, искали наилучшее их расположение, чтобы не так сказывалась Пифагорова комма. Причем это нельзя было сделать раз и навсегда, потому что играли ведь не в одной тональности. Вот и приходилось каждый раз перед концертом приспосабливать лютню к нужным в данном выступлении тональностям.

А настройщики органов, сохраняя чистыми октавы, квинты, а потом и терции, кое-как распределяли Пифагорову комму по другим интервалам, которые от этого получались не совсем чистыми. Музыкант должен был знать заранее, как именно распределена комма и в какой тональности его подстерегают фальшивые звуки. Искусные настройщики умели выходить из положения так. Обычно при игре в двух-трех самых употребительных тональностях некоторые дополнительные звуки, представленные черными клавишами, не используются вообще, остаются как бы в стороне от исполнения. Вот по этим-то звукам и рассовывали комму. Но беда органисту, если он вдруг забудется и возьмет при импровизации какой-нибудь из таких звуков. Тотчас раздается режущая ухо фальшь. Не мудрено, что эти фальшивые звуки были прозваны «волками».

Конечно, музыкантам трудно было смириться с раздражающим неудобством. Особенно досадовали органисты: ведь органу присуща уникальная длительность звука. Одно дело фальшь на лютне, там звук быстро затухает, и совсем другое, когда «волком воет» орган!

Не удивительно поэтому, что именно органист предложил следующую и пока последнюю реформу музыкального строя. Было это в конце семнадцатого века.